Aquí podemos observar como se demuestra la ecuación ordinaria de la parábola que tiene su vértice en el origen.
Consideremos el caso especial en que el vértice es (0,0) y el foco es (0,p). La directriz es por tanto, la recta horizontal que pasa por (0,-p). A la distancia entre el vértice y el foco se le llama distancia focal, de modo que en este caso la distancia focal es igual a p. Con esta configuración se tiene:
La ecuación de una parábola con vértice en (0,0) y foco en (0,p) es |
La ecuación de una parábola con vértice en (0,0) y foco en (0,p) es |
Ambas ecuaciones se refieren a parábolas verticales que se abren «hacia arriba». La ecuación de una parábola que se abre hacia abajo es similar excepto que varía un signo. En este caso, el foco sería (0,-p) y de esta forma:
La ecuación de una parábola con vértice en (0,0) y foco en (0,-p) es |
La ecuación de una parábola con vértice en (0,0) y foco en (p,0) esObteniendo mediante un cambio de signo la ecuación de las parábolas hacia la izquierda.,
 .
. .
.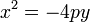 .
.
Me parece muy interesante reforzar lo que nos han dado en clases gracias a los videos... de esta manera podemos complementar lo que se ha enseñado en el aula, ya que hay personas que aprenden mejor de una u otra manera...!!!
ResponderEliminarKATHERINE BARRENO
ResponderEliminareste video me ha servido de ayuda para entender como resolver el ejercicio con facilidad
chido
ResponderEliminar